The ideal constant stepsize of gradient descent
In the aim to compute an approximate solution to the linear inverse problem $\bs{Ax}=\bs y$ with $\bs A \in \Rbb^{n\times n}$ of rank $r \leq n$, one is interested in evaluating the loss
\[\cl L (\bs x^{(k)}, \bs y) = \tinv 2 \|\bs A \bs x^{(k)} -\bs y\|_2^2\]when $\bs x^{(k)}$ is the $k$-th iterate of the Gradient Descent (GD) algorithm with zero initialization. It writes $\bs x^{(k)} = \sum_{i=0}^k (\bs I-\alpha \bs A^* \bs A)^i \alpha \bs A^* \bs y$, and writing the SVD decomposition
\[\bs A := \bs U \bs \Sigma \bs V^*\]with the properties $\bs V^* \bs V = \bs I_r$ and $\bs U^* \bs U = \bs I_r$, one gets
\[\begin{align*} \bs A \bs x^{(k)} &= \sum_{i=0}^k \bs U \bs \Sigma \bs V^* (\bs I_n - \alpha \bs V \bs\Sigma^2 \bs V^*) (\bs I_n - \alpha \bs A^* \bs A)^{i-1} \alpha \bs A^* \bs y \\ &= \sum_{i=0}^k \bs U \bs \Sigma (\bs I_r - \alpha \bs\Sigma^2) \bs V^* (\bs I_n - \alpha \bs A^* \bs A)^{i-1} \alpha \bs A^* \bs y \\ &= \sum_{i=0}^k \bs U \bs \Sigma (\bs I_r - \alpha \bs\Sigma^2)^i \bs V^* \alpha \bs A^* \bs y \\ &= \bs U \bs\Sigma \underbrace{\sum_{i=0}^k (\bs I_r - \alpha \bs\Sigma^2)^i}_{(\alpha \bs\Sigma^2)^{-1} (\bs I_r - (\bs I_r - \alpha \bs\Sigma^2)^{k+1})} \alpha \bs\Sigma \bs U^* \bs y \\ &= \bs U \bs\Sigma^{-1} (\bs I_r - (\bs I_r - \alpha \bs\Sigma^2)^{k+1}) \bs\Sigma \bs U^* \bs y \\ &= \bs U (\bs I_r - (\bs I_r - \alpha \bs\Sigma^2)^{k+1}) \bs U^* \bs y. \end{align*}\]Hence, with \(\alpha \triangleq \frac{\eta}{\|\bs A\|^2}\),
\[\begin{align} \label{eq:loss} \begin{split} \cl L (\bs x^{(k)}, \bs y) &= \tinv 2 \bigg\|\underbrace{(\bs U \bs U^* - \bs I_n) \bs y}_{\perp \text{Im } \bs U } - \bs U \diag \bigg( 1-\eta \big( \frac{\sigma_i}{\sigma_{\mathrm{max}}} \big)^2 \bigg)^{k+1} \bs U^* \bs y \bigg\|_2^2 \\ &= \tinv 2 \bigg\| (\bs U \bs U^* - \bs I_n) \bs y \bigg\|_2^2 + \tinv 2 \bigg\| \bs U \diag \bigg( 1-\eta \big( \frac{\sigma_i}{\sigma_{\rm max}} \big)^2 \bigg)^{k+1} \bs U^* \bs y \bigg\|_2^2 \\ &= \tinv 2 \bigg\| (\bs U \bs U^* - \bs I_n) \bs y \bigg\|_2^2 + \tinv 2 \bigg\| \diag \bigg( 1-\eta \big( \frac{\sigma_i}{\sigma_{\rm max}} \big)^2 \bigg)^{k+1} \bs U^* \bs y \bigg\|_2^2 \\ &\leq \tinv 2 \bigg\| (\bs U \bs U^* - \bs I_n) \bs y \bigg\|_2^2 + \tinv 2 \max_{i \in \upto{r}} \bigg| 1- \eta \big( \frac{\sigma_i}{\sigma_{\rm max}} \big)^2 \bigg|^{2(k+1)} \big\| \bs U^* \bs y \big\|_2^2. \end{split} \end{align}\]The third line is obtained from the second line by using the identity
\[\|\bs{UM} \|_2^2=\langle \bs U \bs M, \bs U \bs M \rangle = \langle \bs U^* \bs U \bs M, \bs M \rangle = \langle \bs M, \bs M \rangle=\|\bs M \|_2^2.\]By convention $\sigma_{\mathrm max} = \sigma_1$. In \eqref{eq:loss}, the first error term is independent of $k$. One cannot do better than targetting the fastest convergence to zero of the second term. For a fixed stepsize $\eta$, the best choice must satisfy
\[\begin{align*} \min_\eta \max_{i \in \upto{r} } \bigg| 1- \eta \big( \frac{\sigma_i}{\sigma_{\rm max}} \big)^2 \bigg| &= \min_\eta \max \bigg( \max_{i \in \upto{r} } 1- \eta \big( \frac{\sigma_i}{\sigma_{\rm max}} \big)^2, \max_{i \in \upto{r} } \eta \big( \frac{\sigma_i}{\sigma_{\rm max}} \big)^2 -1 \bigg) \\ &= \min_\eta \max \bigg( 1- \eta \big( \frac{\sigma_r}{\sigma_{\rm max}} \big)^2,\eta -1 \bigg) \end{align*}\]which is reached when
\[\begin{align} \label{eq:eta} \begin{split} &1 - \eta \big( \frac{\sigma_r}{\sigma_{\rm max}} \big)^2 = \eta - 1 \\ \Leftrightarrow ~& \eta = \frac{2}{1+(\sigma_r/\sigma_1)^2}. \end{split} \end{align}\]One observes that the ideal constant stepsize of the GD method depends only on the ratio between the smallest and the largest singular value which can be associated to the condition number
\[\begin{equation} \label{eq:condition_number} \kappa(\bs A) := \frac{\sigma_1(\bs A)}{\sigma_r (\bs A)}. \end{equation}\]In particular, injecting \eqref{eq:eta} into \eqref{eq:loss} yields
\[\begin{align*} \cl L_k (\bs x^{(k)}, \bs y) &\leq \tinv 2 \bigg\| (\bs U \bs U^* - \bs I_n) \bs y \bigg\|_2^2 + \tinv 2 \big| \eta - 1 \big|^{2(k+1)} \big\| \bs U^* \bs y \big\|_2^2 \\ &= \tinv 2 \bigg\| (\bs U \bs U^* - \bs I_n) \bs y \bigg\|_2^2 + \tinv 2 \bigg| \frac{1-(\sigma_r/\sigma_1)^2 }{1+(\sigma_r/\sigma_1)^2} \bigg|^{2(k+1)} \big\| \bs U^* \bs y \big\|_2^2, \end{align*}\]meaning that the decreasing of the loss with the iterations of the gradient descent is slower when $\sigma_r \ll \sigma_1$.
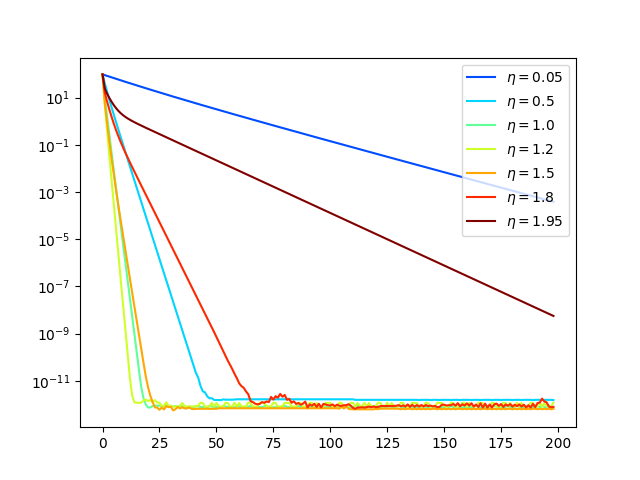
Figure 1: Gradient Descent iterations as a function of the stepsize for the system $\bs A \bs x = \bs y$ with $\bs A \in \Rbb^{30\times 30}$ of rank $r=5$.
In this experiment, the ideal choice following \eqref{eq:eta} was $\eta^\star = 1.26$.