CHSH game and use of entanglement

\[\newcommand{\sqrtt}{\frac{1}{\sqrt 2}} \newcommand{\tinv}[1]{\frac{1}{#1}} \newcommand{\win}{\text{win}} \newcommand{\bb}{\mathbb}\]

Classical CHSH game

The Clauser–Horne–Shimony–Holt (CHSH) game involves two persons, Alice and Bob, who play in collaboration against a referee.

The game setup is illustrated in Fig. 1. Firstly, the referee sends the classical bits $x$ and $y$ to Alice and Bob, respectively, which are randomly drawn from a Bernoulli distribution with

\[\begin{equation} \bb{P}(x=0) = \bb{P}(x=1) = \bb{P}(y=0) = \bb{P}(y=1) = \tinv 2. \end{equation}\]

Alice and Bob cannot communicate together. Secondly, Alice and Bob respectively respond by sending the classical bits $a$ and $b$ to the referee. Alice and Bob win the CHSH game if they manage to satisfy

\[\begin{equation} \label{eq:chsh} x \cdot y = a \oplus b \end{equation}\]

where $\cdot$ is the logical AND (or binary multiplication) and $\oplus$ is the logical XOR (or binary addition).

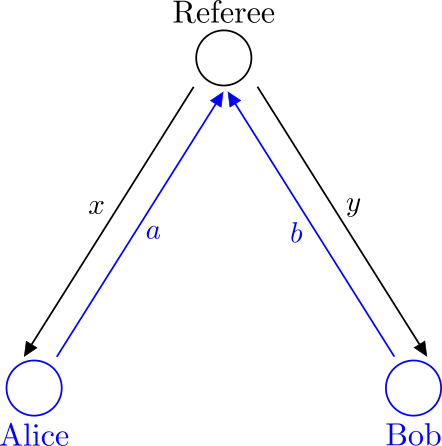
As $x \cdot y = 0$ in 75% of the cases, the simple strategy of Alice and Bob choosing in advance and whatever they mesure $a=0$ and $b=1$ such that $a\oplus b=0$ makes them win in 75% cases. Another strategy where Alice always sends $a=0$ and Bob chooses its bit in function of $y$ as $b=y$ also makes them win in 75% cases. Actually, this winning rate of 75% cannot be beaten, as can be inspected in Table 1 below.

Table 1: All possible combinations in the CHSH game.

$x$	$y$	$a$	$b$	$x\cdot y$	$a\oplus b$	$=$
0	0	0	0	0	0	1
0	0	0	1	0	1	0
0	0	1	0	0	1	0
0	0	1	1	0	0	1
0	1	0	0	0	0	1
0	1	0	1	0	1	0
0	1	1	0	0	1	0
0	1	1	1	0	0	1
1	0	0	0	0	0	1
1	0	0	1	0	1	0
1	0	1	0	0	1	0
1	0	1	1	0	0	1
1	1	0	0	1	0	0
1	1	0	1	1	1	1
1	1	1	0	1	1	1
1	1	1	1	1	0	0

CHSH game with entanglement

Let us now consider the slightly adapted situation illustrated in Fig. 2 where Alice and Bob still cannot communicate together but now share two qbits in the entangled state

\[\begin{equation} \label{eq:entangled} \ket{\psi} = \ket{\Phi^+} = \sqrtt (\ket{00} + \ket{11}). \end{equation}\]

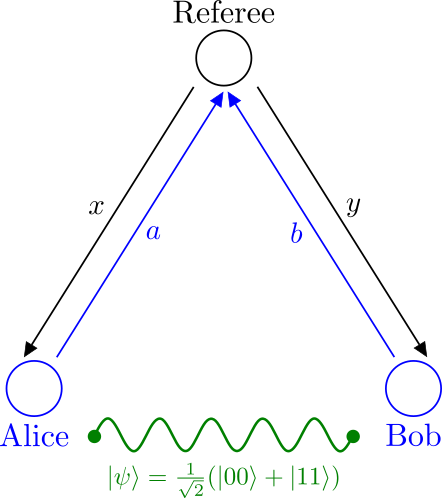
The entangled state $\ket{\psi}$ means that prior to any measurement, both Alice and Bob have equal probabilities to measure a value $\ket{0}$ or $\ket{1}$ on their qbit, but once Alice has measured her qbit in the basis {$0,1$}, the state of Bob’s qbit is completely determined in this basis and vice-versa.

The strategy in this situation contains two ingredients to exploit entanglement.

First ingredient

The first ingredient consists in Alice and Bob measuring their qbit in two different bases.

Indeed, if Alice and Bob measure in the same basis they cannot adapt their response to the referee depending on the bits $x$ (and $y$) they received + their measurement. Even if they measure in another basis, for instance the {$+,-$} basis, there would be no difference with the {$0,1$} basis. This can be demonstrated by decomposing the states $\ket{0}$ and $\ket{1}$ in terms of the $\ket{+}$ and $\ket{-}$ states as \(\begin{equation} \label{eq:+-} \begin{cases} \ket{+} &= \sqrtt (\ket{0} + \ket{1}) \\ \ket{-} &= \sqrtt (\ket{0} - \ket{1}) \\ \end{cases} \Leftrightarrow \begin{cases} \ket{0} &= \sqrtt (\ket{+} + \ket{-}) \\ \ket{1} &= \sqrtt (\ket{+} - \ket{-}) \\ \end{cases}. \end{equation}\)

Injecting \eqref{eq:+-} in \eqref{eq:entangled}, one observes \(\begin{align} \begin{split} \ket{\psi} &= \sqrtt (\ket{00} + \ket{11}) \\ &= \tinv{2\sqrt 2} (\ket{++} + \ket{+-} + \ket{-+} + \ket{--} + \ket{++} - \ket{+-} - \ket{-+} + \ket{--} ) \\ &= \sqrtt (\ket{++} + \ket{--}). \end{split} \end{align}\)

However, if they measure their qbit with a rotation angle $\theta$ with respect to the {$0,1$} basis, for instance Alice measures her qbit in the {$\cos(\theta_A),\sin(\theta_A)$} basis and Bob measures his qbit in the {$\cos(\theta_B), \sin(\theta_B)$} basis with possible measurement results

\[\begin{cases} \ket{\nu_{0A}} &= \cos(\theta_A) \ket{0} + \sin(\theta_A) \ket{1} \\ \ket{\nu_{1A}} &=-\sin(\theta_A) \ket{0} + \cos(\theta_A) \ket{1}, \end{cases}\]

and similarly for Bob, then the possible combinations of outcomes are given as

\[\begin{cases} \braket{\nu_{0A} \nu_{0B}} &= \begin{bmatrix} \cos(\theta_A) \cos(\theta_B) & \cos(\theta_A) \sin(\theta_B) & \sin(\theta_A) \cos(\theta_B) & \sin(\theta_A) \sin(\theta_B) \end{bmatrix} \\ \braket{\nu_{0A} \nu_{1B}} &= \begin{bmatrix} -\cos(\theta_A) \sin(\theta_B) & \cos(\theta_A) \cos(\theta_B) & -\sin(\theta_A) \sin(\theta_B) & \sin(\theta_A) \cos(\theta_B) \end{bmatrix} \\ \braket{\nu_{1A} \nu_{0B}} &= \begin{bmatrix} -\sin(\theta_A) \cos(\theta_B) & -\sin(\theta_A) \sin(\theta_B) & \cos(\theta_A) \cos(\theta_B) & \cos(\theta_A) \sin(\theta_B) \end{bmatrix} \\ \braket{\nu_{1A} \nu_{1B}} &= \begin{bmatrix} \sin(\theta_A) \sin(\theta_B) & -\sin(\theta_A) \cos(\theta_B) & -\cos(\theta_A) \sin(\theta_B) & \cos(\theta_A) \cos(\theta_B) \end{bmatrix} \end{cases}\]

with respective probabilities

\[\begin{cases} (\braket{\nu_{0A} \nu_{0B}| \psi})^2 &=\tinv 2 \cos^2(\theta_A-\theta_B) \\ (\braket{\nu_{0A} \nu_{1B}| \psi})^2 &=\tinv 2 \sin^2(\theta_A-\theta_B) \\ (\braket{\nu_{1A} \nu_{0B}| \psi})^2 &=\tinv 2 \sin^2(\theta_A-\theta_B) \\ (\braket{\nu_{1A} \nu_{1B}| \psi})^2 &=\tinv 2 \cos^2(\theta_A-\theta_B). \end{cases}\]

Second ingredient

The second ingredient consists in Alice and Bob choosing their measurement bases in function of their received bits.

We thus choose

\[\begin{cases} \theta_{A0},~~&\text{if } x=0 \\ \theta_{A1},~~&\text{if } x=1 \\ \theta_{B0},~~&\text{if } y=0 \\ \theta_{B1},~~&\text{if } y=1. \end{cases}\]

Indeed, to maximize their probability of winning against the referee, their goal is to maximize their chances to reach $a \oplus b=0$ if $(x,y) \in$ {$(0,0),(0,1),(1,0)$} and $a \oplus b=1$ if $(x,y)=(1,1)$.

With equal probabilities to receive $(x,y)\in$ {$(0,0),(0,1),(1,0),(1,1)$}, the probability of winning is given as \(\begin{align} \begin{split} \bb P(\win) = &\tinv 4 \bb P(\win|(x,y)=(0,0)) \\ + &\tinv 4 \bb P(\win|(x,y)=(0,1)) \\ + &\tinv 4 \bb P(\win|(x,y)=(1,0)) \\ + &\tinv 4 \bb P(\win|(x,y)=(1,1)). \end{split} \end{align}\)

We have \(\begin{align} \begin{split} \bb P(\win|(x,y)=(0,0)) &= \bb P(\nu_{0A} \nu_{0B} |(x,y)=(0,0)) + \bb P(\nu_{1A} \nu_{1B} |(x,y)=(0,0)) \\ &= (\braket{\nu_{0A} \nu_{0B}| \psi})^2 + (\braket{\nu_{1A} \nu_{1B}| \psi})^2 \\ &= \cos^2(\theta_{A0}-\theta_{B0}), \end{split} \end{align}\)

and similarly \(\begin{align} \bb P(\win|(x,y)=(0,1)) &= \cos^2(\theta_{A0}-\theta_{B1}) \\ \bb P(\win|(x,y)=(1,0)) &= \cos^2(\theta_{A1}-\theta_{B0}) \\ \bb P(\win|(x,y)=(1,1)) &= \sin^2(\theta_{A1}-\theta_{B1}). \end{align}\)

This means that Alice and Bob need to minimize $\theta_A-\theta_B$ when $(x,y) \in$ {$(0,0),(0,1),(1,0)$} and maximize it when $(x,y)=(1,1)$. This optimum is reached if they choose their measurement angles as

\[\begin{cases} \theta_{A0} &= 0 \\ \theta_{A1} &= \frac{\pi}{4} \\ \theta_{B0} &= \frac{\pi}{8} \\ \theta_{B1} &= -\frac{\pi}{8}. \end{cases}\]

With this choice,

\[\begin{cases} \bb P(\win|(x,y)=(0,0)) &= \cos^2(\frac{\pi}{8}) \\ \bb P(\win|(x,y)=(0,1)) &= \cos^2(\frac{\pi}{8}) \\ \bb P(\win|(x,y)=(1,0)) &= \cos^2(\frac{\pi}{8}) \\ \bb P(\win|(x,y)=(1,1)) &= \sin^2(\frac{3\pi}{8}) = \cos^2(\frac{\pi}{8}) \end{cases}\]

so that

\[\begin{equation} \label{eq:p_win} \bb P(\win) = \cos^2 (\pi/8) \approx 85 \%. \end{equation}\]

What \eqref{eq:p_win} demonstrates is that Alice and Bob have been able to exploit the two entangled qbits they shared in order to increase their probability of winning the CHSH game, passing from 75% to 85%!

This result an example of application of the famous Bell's inequality, coming soon in this blog.