Simple proof of the Fourier-slice theorem

\[\newcommand{\im}{\mathrm{i}} \newcommand{\bs}{\boldsymbol} \newcommand{\cl}{\mathcal} \newcommand{\ud}{\mathrm{d}} % Infinitesimal part for integration \newcommand{\Rbb}{\mathbb{R}} \newcommand{\Cbb}{\mathbb{C}} \newcommand{\tinv}[1]{\frac{1}{#1}} \newcommand{\intfty}{\int_{-\infty}^\infty} \newcommand{\iintfty}{\iint_{-\infty}^\infty} \newcommand{\so}{\sin (\theta)} % sin(theta) \newcommand{\co}{\cos (\theta)} 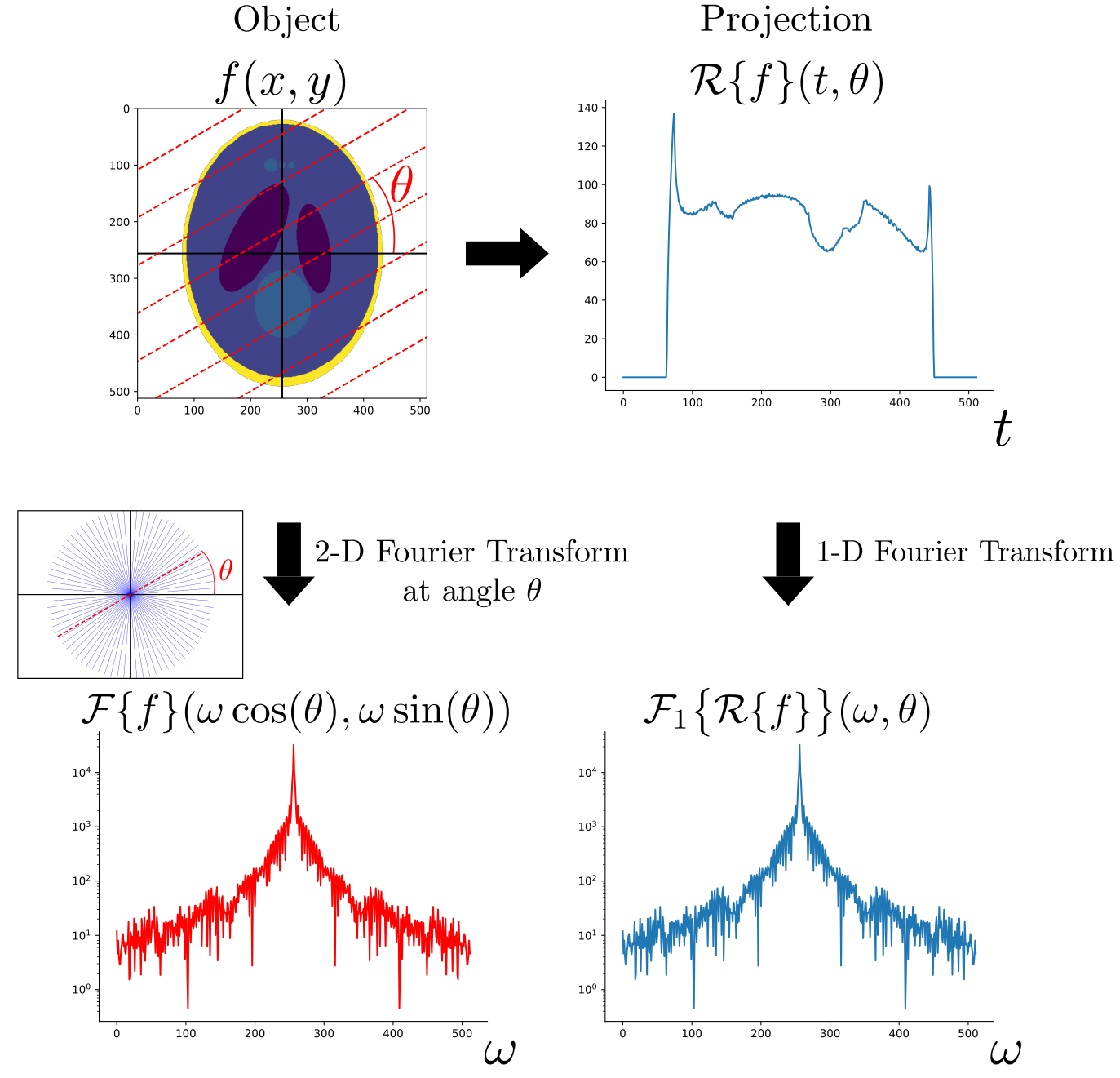% cos(theta)\]

Definition. (Radon transform) The Radon transform \(\cl R \{f\}\) of $f: \Rbb^2 \rightarrow \Rbb$ is \(\begin{equation} \label{eq:radon} \cl R \{f\}(t, \theta) = \iintfty f(x,y) \delta(t-x \co - y \so) \ud x \ud y, \end{equation}\) for $t \in \Rbb$ and $0\le \theta < \pi$.

We wish to prove the Fourier-Slice Theorem reminded in p.37 of (Adcock & Hansen, 2021)

\[\begin{equation} \label{eq:fourier_slice} \cl{F}_1 \big\{ \cl R \{ f \} \big\} (\omega, \theta) = \cl F \{ f \} (\omega \co, \omega \so),~~~~\omega \in \Rbb,~ \theta \in [0,2\pi) \end{equation}\]

Where $\cl F$ denotes the 2-D Fourier transform and $\cl F_1$ is the 1-D Fourier transform with respect to the first component.

proof.

Using \eqref{eq:radon} and the definition of the Fourier transform, the left term of \eqref{eq:fourier_slice} writes as

\[\begin{align} \label{eq:left} \cl{F}_1 \big\{ \cl R \{ f \} \big\} (\omega, \theta) &= \intfty \left( \iintfty f(x,y) \delta(t-x \co -y \so) \ud x \ud y \right) e^{-\im \omega t} \ud t \\ &= \iintfty f(x,y) \big( \intfty \delta(t-x \co -y \so) e^{-\im \omega t} \ud t \big) \ud x \ud y \\ &= \iintfty f(x,y) \big( \intfty \delta(t-x \co -y \so) e^{-\im \omega (x \co+y\so)} \ud t \big) \ud x \ud y \\ &= \iintfty f(x,y) e^{-\im \omega (x \co+y\so)} \underbrace{\big(\intfty \delta(t-x \co -y \so) \ud t \big)}_{=1} \ud x \ud y \\ &= \iintfty f(x,y) e^{-\im \omega (x \co+y\so)} \ud x \ud y \\ &= \cl F \{ f \} (\omega \co, \omega \so) \end{align}\]

which proves \eqref{eq:fourier_slice}. □

References

2021

1. Compressive imaging: structure, sampling, learning

   Ben Adcock and Anders C Hansen

   2021