Moreau envelope, Proximal Operator, and Soft-Thresholding

\[\newcommand{\im}{\mathrm{i}\mkern1mu} \newcommand{\bs}{\boldsymbol} \newcommand{\cl}{\mathcal} \newcommand{\ud}{\mathrm{d}} \newcommand{\Rbb}{\mathbb{R}} \newcommand{\Cbb}{\mathbb{C}} \newcommand{\tinv}[1]{\frac{1}{#1}}\]

Definition. (Moreau envelope) Let $f: \Rbb^n \rightarrow (-\infty, +\infty]$ be a proper, lower semi-continuous, convex function. For a parameter $\lambda > 0$, the Moreau envelope of $f$ with index $\lambda$ is defined as

\[\begin{equation} \label{eq:moreau} \mathrm{M}_\lambda f(x) = \inf_{y\in \Rbb^n} \left\{ f(y) + \tinv{2\lambda} \| x-y \|_2^2 \right\}. \end{equation}\]

This can be seen as a “smoothed” version of $f$, obtained by infimal convolution with the squared norm. Closely related is the proximal operator:

\[\begin{equation} \label{eq:prox} \mathrm{prox}_{\lambda f} (x) := \mathrm{argmin}_{y \in \Rbb^n} \big\{ f(y) + \tinv{2\lambda} \| x-y \|_2^2 \big\}. \end{equation}\]

From \eqref{eq:moreau} and \eqref{eq:prox}, the Moreau enveloppe can be expressed as:

\[\begin{equation} \label{eq:3} \mathrm{M}_\lambda f(x) = f(\mathrm{prox}_{\lambda f} (x)) + \tinv{2\lambda} \| x-\mathrm{prox}_{\lambda f} (x) \|_2^2. \end{equation}\]

Example: the absolute value:

Particularizing \eqref{eq:moreau} to $$f(x)=

x

$$ yields

\[\begin{align} \mathrm{prox}_{\lambda|\cdot|} (x) &= \mathrm{argmin}_{y\in \Rbb^n} \left\{ |y| + \tinv{2 \lambda} (x-y)^2 \right\} \\ &= \mathrm{argmin}_{y\in \Rbb^n} \begin{cases} &y + \tinv{2 \lambda} (x-y)^2,~~y>0 \\ &-y + \tinv{2 \lambda} (x-y)^2,~~y<0 \\ \end{cases} \\ &\Leftrightarrow \begin{cases} &\lambda + y-x = 0,~~y>0 \\ &-\lambda + y-x = 0,~~y<0 \\ \end{cases} \\ &\Leftrightarrow \begin{cases} &y = x-\lambda,~~x>\lambda \\ &y = x+\lambda,~~x<-\lambda \\ &y=0,~~\mathrm{otherwise.} \end{cases} \label{eq:7}. \end{align}\]

The solution in \eqref{eq:7} can be synthesized as:

\[\begin{equation} \label{eq:soft} \mathrm{prox}_{\lambda|\cdot|} (x) = \mathrm{sign}(x) \max \{ |x| - \lambda, 0 \}. \end{equation}\]

The result in \eqref{eq:soft} is the 1-D case of the well-known Soft-thresholding operator \(\cl S_\lambda = \mathrm{prox}_{\lambda \| \cdot \|_1}\).

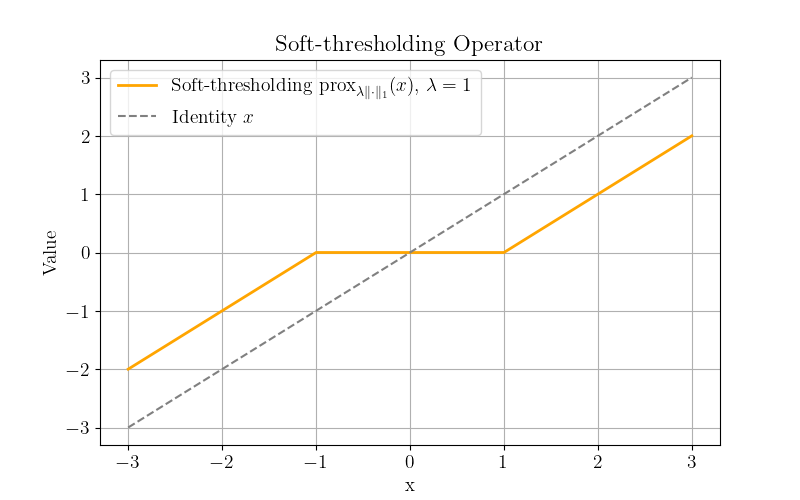
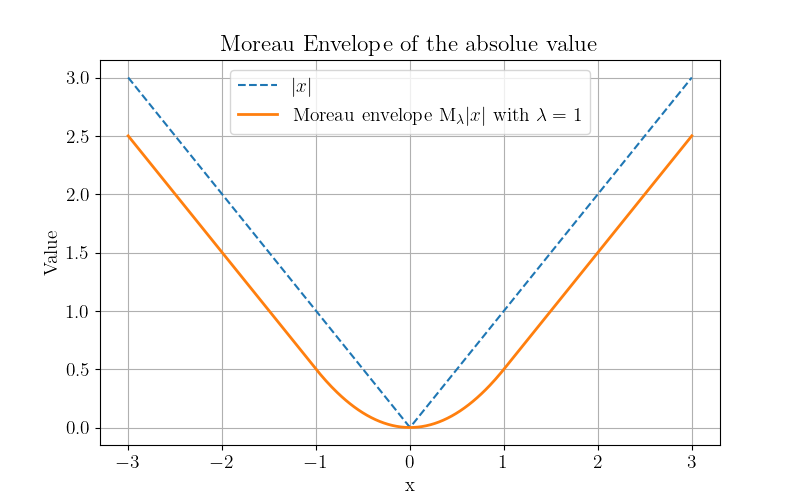
Finally, by injecting \eqref{eq:soft} into \eqref{eq:3}, the Moreau envelope of the absolute value function can be written as

\[\begin{align} \mathrm{M}_\lambda |x| &= |\mathrm{sign}(x) \max\{ |x|-\lambda,0 \}| + \tinv{2\lambda} (x-\mathrm{sign}(x) \max\{ |x|-\lambda,0 \})^2 \\ &= \begin{cases} &\tinv{2\lambda} x^2,~~|x|\le \lambda, \\ &x-\frac{\lambda}{2},~~x>\lambda \\ &-x-\frac{\lambda}{2},~~x<-\lambda \\ \end{cases} \\ &= \begin{cases} &\tinv{2\lambda} x^2,~~|x|\le \lambda, \\ &|x|-\frac{\lambda}{2},~~|x|> \lambda, \\ \end{cases}. \end{align}\]

---

The soft-thresholding operator is of great interest because it is often involved in minimization problems of the form

\[\begin{equation} \label{eq:inv_prob} \tilde{\bs x} = \mathrm{argmin}_{\bs x} \tinv 2 \| \bs y - \bs{Ax} \|_2^2 + \lambda \| \bs x \|_1, \end{equation}\]

where \(\lambda \| \bs x \|_1\) is a convex but nondifferentiable function so that we cannot compute their gradient. Eq. \eqref{eq:inv*prob} can be solved efficiently by the proximal gradient method (PGM) that consists of alternating because a gradient descent step with respect to the differentiable function and a proximal step with respect to the nondifferentiable function(s). For instance, \eqref{eq:inv_prob} can be solved by the iterations

\[\begin{equation} \bs x^{(k+1)} = \cl S_\lambda \big(\bs x^{(k)} - \alpha \bs A^* (\bs{Ax}^{(k)} - \bs y) \big). \end{equation}\]