Quantum bit teleportation

Let us consider the situation where a first person Alice wants to teleports her qbit state to another person Bob. Let us write $A_1$ the qbit that Alice wants to teleports to Bob. To do so, Alice needs a second qbit $A_2$ which must be entangled with one qbit owned by Bob. The situation is illustrated in Fig. 1.

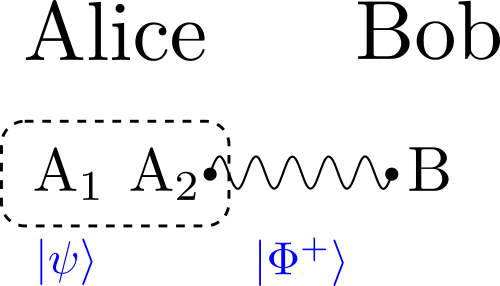
Firstly, let us write $\ket{\psi} = \alpha \ket{0} + \beta \ket{1}$ the state of the qbit $A_1$.
Secondly, $A_2$ and $B$ are entangled as: \(\begin{equation} \ket{A_2 B} = \sqrtt (\ket{00} + \ket{11}) = \ket{\Phi^+}. \end{equation}\)

The total initial state is: \(\begin{equation} \ket{\psi}_{A_1} \ket{\Phi^+}_{A_2 B} = ( \alpha \ket{0} + \beta \ket{1} ) \sqrtt (\ket{00} + \ket{11}) = \sqrtt \big[ \alpha(\ket{000} + \ket{011}) + \beta (\ket{100} + \ket{111}) \big]. \end{equation}\)

The key action for teleporting the qbit is that Alice measures her two qbits in the Bell basis: \(\begin{equation} \ket{\Phi^{\pm}} = \sqrtt (\ket{00} \pm \ket{11}),~~\ket{\Psi^{\pm}} = \sqrtt (\ket{01} \pm \ket{10}) \end{equation}\) which implies \(\begin{align} \begin{split} \ket{00} = \sqrtt (\ket{\Phi^+} + \ket{\Phi^-}),~~&\ket{11} = \sqrtt (\ket{\Phi^+ - \ket{\Phi^-}}) \\ \ket{01} = \sqrtt (\ket{\Psi^+} + \ket{\Psi^-}),~~&\ket{10} = \sqrtt (\ket{\Psi^+ - \ket{\Psi^-}}). \end{split} \end{align}\)

Rewriting the total initial state with the two qbits $A_1,~A_2$ of Alice written in the Bell basis gives: \(\begin{align} \ket{\psi}_{A_1} \ket{\Phi^+}_{A_2 B} &= \frac{1}{2} \big[ \alpha (\ket{\Phi^+} \ket{0} + \ket{\Phi^-} \ket{0} + \ket{\Psi^+} \ket{1} + \ket{\Psi^-} \ket{1}) + \beta (\ket{\Psi^+} \ket{0} - \ket{\Psi^-} \ket{0} + \ket{\Phi^+} \ket{1} - \ket{\Phi^-} \ket{1}) \big] \\ &= \frac{1}{2} \big[ \ket{\Phi^+} (\alpha \ket{0} + \beta \ket{1}) + \ket{\Phi^-} (\alpha \ket{0} - \beta \ket{1}) + \ket{\Psi^+} (\alpha \ket{1} + \beta \ket{0}) + \ket{\Psi^-} (\alpha \ket{1} - \beta \ket{0}) \big] \\ &= \frac{1}{2} \big[ \ket{\Phi^+}_{A_1 A_2} \ket{\psi}_B + \ket{\Phi^-}_{A_1 A_2} Z \ket{\psi}_B + \ket{\Psi^+}_{A_1 A_2} X \ket{\psi}_B + \ket{\Psi^-}_{A_1 A_2} ZX \ket{\psi}_B \big]. \label{eq:7} \end{align}\)

In a final step, Alice sends her 2-qbit measurement among the four possibilities $[\ket{\Phi^\pm}, \ket{\Psi^\pm}]$ to Bob who can now deduce which version of $\ket{\psi}$ he obtained among the possibilities $[\ket{\psi}, Z \ket{\psi}, X \ket{\psi}, ZX \ket{\psi}]$.

In conclusion, \eqref{eq:7} demonstrates that Alice and Bob traded one qbit $A_1$, one entangled state between $A_2$ and $B$, and paid the classical transfer of Alice’s measurement in order to teleport the state $\ket{\psi}$ initially stored in $A_1$ to Bob’s qbit $B$.